Evaluation et diminution de l'incertitude
Phométrie d'ouverture
Détermination du l'ouverture optimale
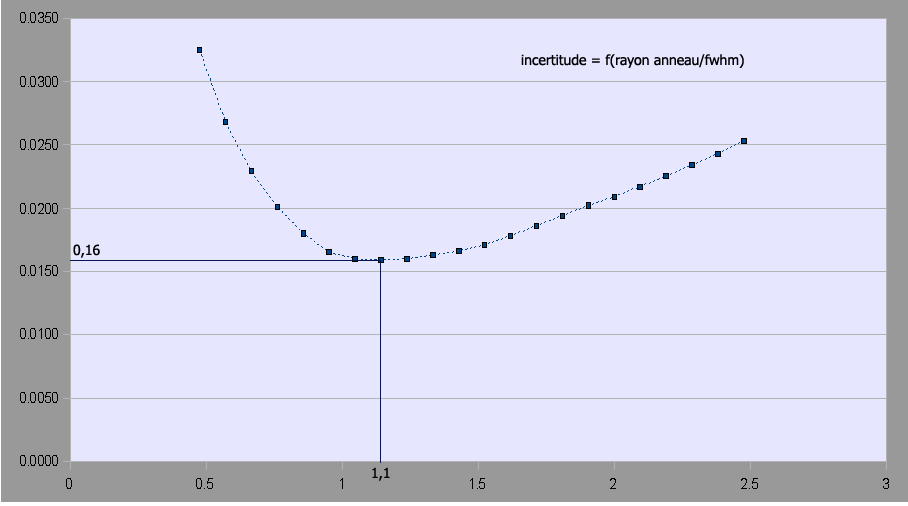
Image : HO DEL 12 08 2008 Exposition : 30 secondes - Pas de filtre - Mesure du SNR sur HO Del
On fait varier le rayon du cercle intérieur de mesure sur une étoile et l'on reléve l'incertitude (ERROR) calculée par le logiciel (en ordonnée).
L'abcisse représente le rapport entre l'ouverture du cercle de mesure et la FWHM.
La FWHM mesurée sur l'image est de 2,1.
En théorie, le rapport donnant le meilleur SNR est 0,8. On constate sur cet exemple qu'une valeur légérement supérieure (1,1) fournit la mesure optimale.
On remarque également que l'erreur augmente rapidement si l'ouverture de l'anneau de mesure est trop faible : mieux vaut un anneau un trop grand que trop petit.
Incertitude en fonction de la magnitude
L'estimation théorique de l'Incertitude est fournie par les logociels de mesure photométrique. Nous nous proposons de déterminer expérimentalement l'incertitude réelle et de la comparer à la théorie.
Méthode : 30 images traitées du champ de AM Herculis sont traitées avec MIRA. Chaque image a un temps d'acquisition de 30 secondes, filtre Vert et a été traitée dans MaximDL (Dark et Flat).
Nombre d'images :
30 images permettent d'obtenir des valeurs statistiques significatives
L'étoile 122 est choisie comme référence [voir Photométrie AM Her] . Une vingtaine d' étoiles sont choisies de façon aléatoire (des plus brillantes aux plus faibles) La réduction photométrique est effectuée sur les 23 étoiles pour les 30 images. Le résultat est exporté dans OpenOffice pour exploitation. Après avoir trié le fichier par étoile (Object), on calcule pour chaque étoile : la magnitude moyenne, l'écart-type des mesures et la moyenne des SNR.
L'écart-type sur les mesures de chaque étoile permet de déterminer l'incertitude expérimentale, réelle, tenant compte de l'ensemble des facteurs influançant la mesure.
On reporte ces valeurs dans un tableau.
| Etoile | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| Moyenne | 13.098 | 14.718 | 13.172 | 15.909 | 14.298 | 15.470 | 14.057 | 14.184 | 15.504 | 14.741 | 15.304 | 14.815 | 14.955 | 15.814 | 16.007 | 13.596 | 14.543 | 13.934 | 14.244 | 14.627 | 14.819 | 14.120 | 15.590 |
| Écart-type | 0.020 | 0.090 | 0.021 | 0.308 | 0.059 | 0.176 | 0.048 | 0.067 | 0.187 | 0.113 | 0.142 | 0.106 | 0.105 | 0.235 | 0.251 | 0.034 | 0.082 | 0.044 | 0.068 | 0.079 | 0.110 | 0.042 | 0.225 |
| Moyenne SNR | 112.84 | 38.23 | 106.1 | 11.72 | 41.96 | 16.58 | 52.56 | 46.37 | 15.51 | 29.01 | 17.97 | 27.25 | 23.89 | 11.15 | 11.79 | 76.14 | 35.44 | 58.15 | 44.63 | 31.36 | 27.98 | 48.83 | 13.95 |
| 2,5 * log(1+1/SNR) | 0.019 | 0.055 | 0.020 | 0.171 | 0.051 | 0.124 | 0.041 | 0.046 | 0.132 | 0.072 | 0.115 | 0.077 | 0.087 | 0.179 | 0.170 | 0.028 | 0.060 | 0.037 | 0.048 | 0.067 | 0.075 | 0.044 | 0.145 |
| 2,5 * log(1+2/SNR) | 0.026 | 0.062 | 0.027 | 0.178 | 0.058 | 0.131 | 0.048 | 0.053 | 0.139 | 0.079 | 0.122 | 0.084 | 0.094 | 0.186 | 0.177 | 0.035 | 0.067 | 0.044 | 0.055 | 0.074 | 0.082 | 0.051 | 0.152 |
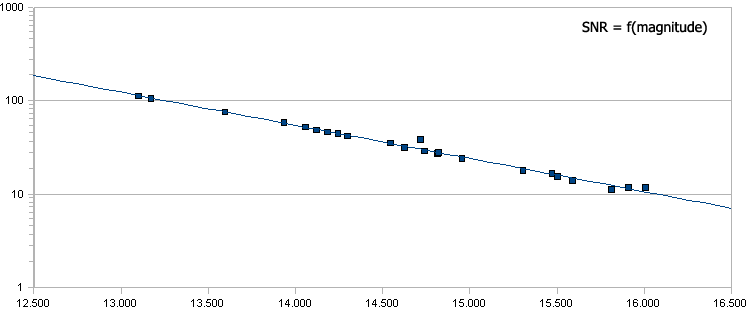
Les lignes 1 et 3 permettent de construire le graphique : SNR en fonction de la magnitude. L'échelle est logarithmique. Le SNR de 100, correspondant à une mesure de bonne précision théorique (1%) est obtenu pour une magnitude de 13,25 environ. Le SNR est de 10 (précision de 10%) correspond à la magnitude 16,1.
Le SNR permet de calculer l'incertitude sur la mesure.
La formule la plus simple est approchée. Elle est valable pour un signal fort par rapport au fond du ciel, c'est à dire pour les étoiles brillantes.
s = 1/SNR [1]
La formule plus précise est :
s = 2,5 * log (1 + 1/SNR) [2]
C'est la valeur ERROR(T) fournie par MIRA DL
Mira calcule également une incertitude dénommée ERROR et correspondant approximativement à 1,6 * error(T) Cette incertitude est une meilleure évaluation de l'incertitude réelle. |
 |
En pratique, l'on constate qu'aucune des deux n'est une bonne évaluation de l'erreur expérimentale qui est sous-estimée :
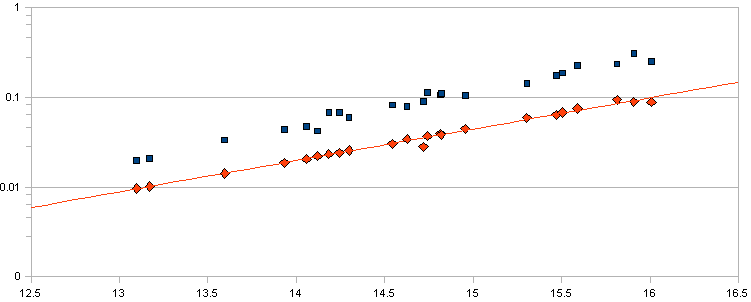 |
Ce graphique présente l'incertitude théorique calculée à partir du SNR (formule [2]) en rouge et l'incertitude réelle déterminée par la détermination des écart-type sur les mesures. On constate que la formule 2 donnant la valeur ERROR(T) de MIRA DL sous-estime nettement l'incertitude |
Pour une estimation conservative de l'incertitude, il est donc préférable de choisir la formule :
s = 2,5 * log (1+2/SNR) [3]
qui permet de calculer l'incertitude à 95% de confiance, alors que la formule [2] fournit l'incertitude à 68% de confiance.
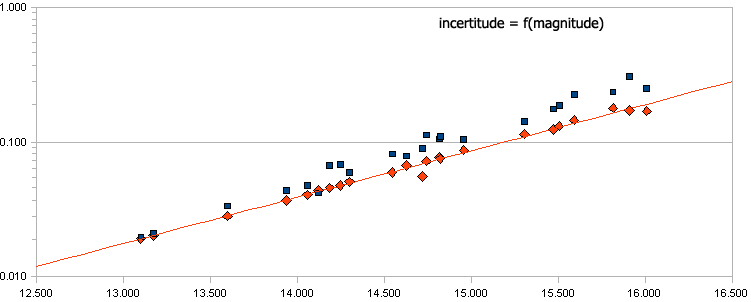 |
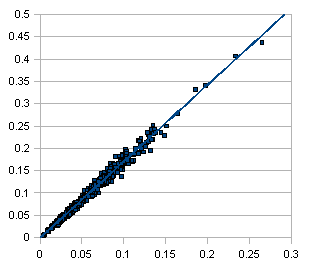
Graphique représentant l'incertitude théorique calculée à partiur du SNR suivant la formule [3] à 95% de confiance en Rouge et l'incertitude expérimentale réelle en Bleu |
On obtient donc une estimation conservative, moins , mais plus représentative de la réalité, par la formule
s = 2,5 log(1+2/SNR)
Avec le matériel utilisé, on obtient, pour un temps de pose de 30 secondes l'estimation suivante de l'incertitude expérimentale :
s = 1,213 * 10-7 * 2,508 Mag
|
Graphique représentant l'incertitude réellement mesurée en fonction de la magnitude |
Amélioration (diminution de l'incertitude)
Avec le matériel utilisé, la précision founie par la photométrie d'une image reste convenable (5% d'incertitude) jusqu'à la magnitude 13,5 - 14. Elle augmente ensuite rapidement.
A matériel et traitement identique, l'incertitude peut être diminuée
- en augmentant le temps de pose (ce qui implique soit de diminuer les erreurs périodiques de suivi de la monture soit d'autoguider)
- en compositant les images.Compositage des images et incertitude
Cette technique permet d'améliorer l'incertitude en fonction de la racine carrée du nombre d'image
On a : SNR[n] = SNR[1] * racine_carrée (n)
avec SNR[n]= SNR mesuré sur une image résultant du compositage de n images différentes
Méthode : à partir d'une série d'images (ici AM Her), on réalise des compositages successifs de 1, 2, 4, 8, 16, 32, ... images puis l'on détermine le SNR et l'incertitude pour plusieurs étoiles.
1 2 4 8 16 32 12.0 280 396 560 792 1121 1585 12.5 186 263 372 526 744 1053 13.0 124 175 247 350 494 699 13.5 82 116 164 232 328 464 14.0 55 77 109 154 218 308 14.5 36 51 72 102 145 205 15.0 24 34 48 68 96 136 15.5 16 23 32 45 64 90 16.0 11 15 21 30 42 60 16.5 7 10 14 20 28 40 17.0 5 7 9 13 19 26 SNR mesuré en fonction de la magnitude et du nombre d'images compositées
Incertitude sur la moyenne
Pour une distribution gaussienne de mesures et un nombre suffisemment grand de mesures , l'incertitude sur la moyenne, à 95% de confiance est donnée par :
i = 2 * s / racine (N) [3]
s étant l'écartype des mesures et N le nombre de mesures
Le facteur 2 est une approximation pour un nombre important de mesures (>30)
De façon plus précise, il est préférable d'utiliser le facteur de Student, dont les valeurs, pour un degré de confiance de 95% est :
N
4
8
16
30
Infini
t95
3.18
2.37
2.13
2.04
1.96
La formule [3] devient :
i = t95 * s / racine (N) [4]
D'autre part, à la probabilité de 95%, les valeurs mesurées sont comprises dans l'intervalle [m-2s;m+2s]
( ou encore, 19 valeurs sur 20 sont comprises dans cet intevalle)
Données : 16 images de GY Cnc prises le 24 03 2009.suffisemment grand de mesures.
La magnitude de 5 étoiles est déterminée pour chacune des images en prenant 000-BBQ-315 comme référence (mag V = 11.002). voir GY Cnc
Pour chacune des étoiles, on calcule : la moyenne des mesures, l'écart-type, le maximum, le minimum, puis l'incertitude sur la moyenne (formule [3])
réf. IAUD 000-BBQ-292 000-BBQ-308 000-BBQ-299 000-BBQ-319 000-BBQ-317 m
moyenne 11.253 11.543 13.410 14.500 15.375 s écart-type 0.011 0.009 0.026 0.046 0.175 i incertitude 0.005 0.005 0.013 0.023 0.087 max maximum 11.271 11.557 13.449 14.566 15.815 min minimum 11.235 11.529 13.364 14.414 15.149 D max-min 0.035 0.028 0.085 0.151 0.665 4 * s 0.044 0.037 0.105 0.182 0.699 L'incertitude i sur la moyenne est calculée par la formule [3]
On constate que l'intervalle 4 * s encadre bien l'intervalle des valeurs max-min.Représentation graphique pour 000-BBQ-299
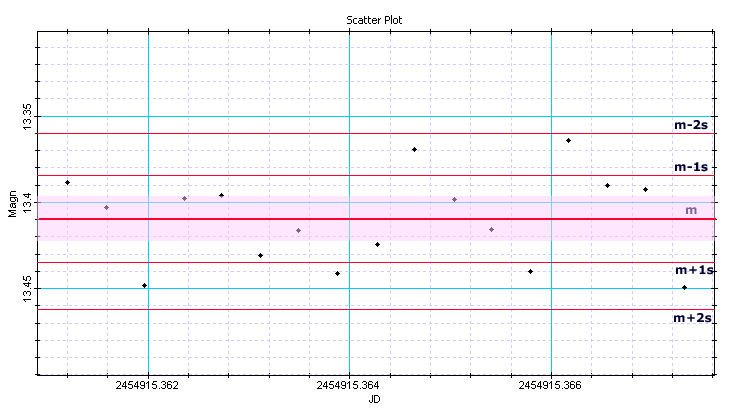
La zone rose correspond à l'incertitude affectant la moyenne calculée (m = 14.10 +/- 0.013 )
Toutes les mesures sont comprises dans l'intervalle [m-2s;m+2s]Comparaison des méthode d'addition
Matériel et logiciels
Télescope LX200 10"
Caméra CCD Starlight SXV H9
Filtres Schuller BVRAcquisition - Réduction : MaximDL
Photométrie : MIRA AP (Mirametrics) et MIRA PRO
Calcul : Open Office
Bibliographie
A pratical guide to Lightcurve and Analaysis, B. Warner, Springer, 2006
CCD Observing Manuel, AAVSO http://www.aavso.org/observing/programs/ccd/manual/
Estimating photometry errors, B. Gary http://reductionism.net.seanic.net/Astrophotos/SE/SE.htm
Exoplanet observing for amateurs, B. Gary http://brucegary.net/book_EOA/x.htm
Blazar "W COM" Monitoring feasability demonstration, B. Gary http://reductionism.net.seanic.net/Astrophotos/BLAZARS/w_com.htm
Introduction to astronomical photometry using CCD, Romanishin http://observatory.ou.edu/wrccd22oct06.pdf